单纯型法
数学模型
- 决策变量 $X=(x_1,x_2,\cdots,x_n)^T$ $x_j \ge 0$
- 约束条件 $\sum_{j=1}^n a_ijx_j \le b_i$ $i=1,2,\cdots,m$
- 目标函数 $max(min)Z=\sum_{j=1}^n c_jx_j$
标准型
- 资源限量 $b_i \ge 0$
- 价值向量 $\bf{C} = (c_1,c_2,\cdots,c_n)^T$
化解步骤
- 目标函数最大。最小值时,要把目标函数的符号反转$Z’ = -Z$
- 资源限量非负 $b_i \ge 0$,对于不大于零的式子,要乘以$-1$
- 约束条件等式 对于有小于等于的等式,要加上松弛变量,例如:$-2x_1+x_2+x_3 \le 9$ 变为 $-2x_1+x_2+x_3+x_4 = 9$。对于包含大于等于的式子,要减去剩余变量,例如:$x_1+x_2+x_3 \ge 5$ 变为 $x_1+x_2+x_3-x_5 = 5$。松弛变量与剩余变量分别表示未被充分利用的资源,但是价值系数保持为0。
- 决策变量非负 对于$x_j \le 0$,要换成一个变量$x_j’ = -x_j$。对于无约束的变量$x_k$,引入两个新的变量$x_k’,x_k’’$,将$x_k$转化为$x_k’-x_k’’$。其中$x_k’\ge 0,x_k’‘\ge 0$。
解的概念
- 约束条件等式所构成的增广矩阵$\bf A $为满秩矩阵。
- 如果能够找到一个$\bf B$,使得$\bf B$为$\bf A $的满秩子矩阵,那么称$\bf B$为线性规划的一个基。
- 方程有n-m个自由变量
- 假设前m个变量的基向量为其系数向量,那么有$\sum_{i=1}^n \bf{a_i} x_i = \bf b $,则有$\sum_{i=1}^m \bf{a_i} x_i = \bf b - \sum_{i=m+1}^n \bf{a_i} x_i$,可以将原来的$\bf X$ 化为$\bf X= (X_B,X_N)$
单纯型法的步骤
- 两阶段法这个网站讲的很好,按照这个例题来https://blog.csdn.net/se511/article/details/9042027,可以使用这个网站辅助计算https://www.mathstools.com/section/main/simplex_online_calculator#
算法复杂度分析
三种复杂度
-
$f(n) \in O(g(n))$ 表示 $ f(n) \le k g(n)$ -
$f(n) \in \Omega(g(n))$ 表示 $ f(n) \ge k g(n)$ - $f(n) \in \Theta(g(n))$ 表示 $|f(n)| = k g(n)$
复杂度运算法则
- $O(f)+O(g) = O(max(f,g))=O(f+g)$
- $O(f)O(g) = O(f \cdot g)$
主定理
在算法分析中,主定理(Master Theorem) 是用于求解形如递归关系式的时间复杂度的重要工具,尤其适用于分治算法的复杂度分析。下面将从定理内容、应用条件、常见案例及注意事项等方面详细介绍。
主定理的形式与定义
主定理用于求解以下形式的递归关系式: \(T(n) = a \cdot T\left(\frac{n}{b}\right) + f(n)\) 其中:
- n 为问题规模;
- a 为递归调用的次数($a \geq 1$);
- $\frac{n}{b}$ 为每个子问题的规模($b > 1$,通常为整数);
- $f(n)$ 为递归外的计算成本(如合并子问题解的时间)。
主定理根据 $f(n)$ 与 $n^{\log_b a}$ 的增长关系,将复杂度分为三种情况:
主定理的三种情况
假设 $c = \log_b a$,则:
- 情况一:$f(n) = O(n^{c - \varepsilon})$($\varepsilon > 0$ 为常数)
- 此时,递归项主导,复杂度为: \(T(n) = \Theta(n^c) = \Theta(n^{\log_b a})\)
- 直观理解:$f(n)$ 的增长速度显著慢于 $n^c$,子问题的递归成本占主导。
- 情况二:$f(n) = \Theta(n^c \cdot \log^k n)$($k \geq 0$ 为常数)
- 此时,递归项与 $f(n)$ 增长速度相当,复杂度为: \(T(n) = \Theta(n^c \cdot \log^{k+1} n)\)
- 常见子情况:
- 当 $k=0$ 时,$f(n) = \Theta(n^c)$,则 $T(n) = \Theta(n^c \cdot \log n)$。
- 情况三:$f(n) = \Omega(n^{c + \varepsilon})$($\varepsilon > 0$ 为常数),且满足正则条件 $a \cdot f(n/b) \leq k \cdot f(n)$($k < 1$ 为常数)
- 此时,非递归项主导,复杂度为: \(T(n) = \Theta(f(n))\)
- 正则条件说明:确保 $f(n)$ 的增长足够快,避免递归项对其主导性的影响(例如 $f(n)$ 不能是指数级震荡函数)。
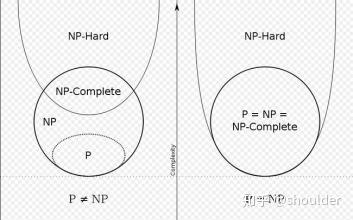
NP完全问题
P问题
所有可以在多项式时间内用确定性算法求解的问题,如排序、最短路径等。
NP问题
- 对于问题的任意一个可能解,存在一个多项式时间的验证算法(即验证时间为 $O(n^k)$,其中 $k$ 为常数),但不存在一个多项式时间的解算法。为常数),能够判断该解是否为正确解。 - 或者从非确定性图灵机的角度定义:可以在非确定性多项式时间内求解的问题(非确定性图灵机可理解为能 “猜测” 正确解并验证的抽象计算模型)。 - NP 类问题的求解可能需要指数级时间(如穷举搜索),但**验证**一个解的正确性仅需多项式时间。 ### NPC(NP-complete)问题 - 首先,它得是一个NP问题; - 然后,所有的NP问题都可以约化到它。 ### NP-Hard问题 是这样一种问题,它满足NPC问题定义的第二条但不一定要满足第一条(就是说,NP-Hard问题要比 NPC问题的范围广,NP-Hard问题没有限定属于NP),即所有的NP问题都能约化到它,但是它不一定是一个NP问题。